Horizon 1995-1996: Fermat’s Last Theorem Review

The Story of Fermat’s Last Theorem

Fermat’s Last Theorem was the most famous mathematical problem of the twentieth century and has appeared countless times in popular culture. Fermat’ Theorem is deceptively simple. The equation above is a more general version of an equation we all know, Pythagoras’ theorem, which is x² + y² = z². When studying Pythagoras’ Theorem we learn about some special cases in his theorem called Pythagorean triples which is when x, y and z all have integer solutions. Examples of these include, 3,4,5 and 5,12,13 and 8,15,17. Fermat being an excellent inquisitive mathematician asked what happens when I change n? Can I still get integer solutions? Fermat owned a copy of the book Arithmetica by the Ancient Greek mathematician Diophantus. Diophantus explored many ideas like this and Fermat wrote incredibly insightful notes in the margin. In Artithmetica Diophantus ponders are there any integer solutions for x, y and z, for xⁿ + yⁿ = zⁿ except when n=2. Fermat wrote in the margin that the equation only holds when n=2. He then stated he had a truly marvellous proof for this, but the margin was too small to contain it. Very Helpful!

After Fermat died and his works were published many top mathematicians tried to prove his conjecture. However, it proved much harder than expected. Some of the most famous mathematicians such as Gauss and Euler could not prove his conjecture. In fact, Euler was so frustrated by the problem he asked people to search Fermat's house for any scrap of paper that may help him prove the theorem

After that 100 years passed, with many unsuccessful attempts at solving his theorem, until Lamé believed he solved it in 1847. His proof relied on using complex numbers to factorise the equation of Fermat’s theorem. However, as pointed out by Kummer, Lamé’s proof was wrong. The issue came with the complex numbers.  One of the most important facts about the positive integers is that they have a unique prime factorisation. This is the fundamental theorem of arithmetic. However, do complex numbers have a unique prime factorisation? Lamé thought so, but Kummer was less sure. The debate raged on until 6 months later Kummer found a complex number that has two different prime factorisations. After this Fermat’s last theorem almost fell out of fashion for another 100 years.

In Japan in the 1950s a breakthrough occurred that would rekindle the interest in Fermat’s Last Theorem. Goro Shimura and Yutaka Taniyama began studying something called modular forms, which put simply are a special variety of object with immensely high symmetry and complexity. 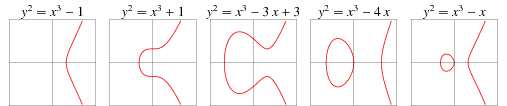The duo came to the realisation that the ingredients for constructing different modular forms were encoded in the solutions to a particular set of equations, known as elliptic curves. These are simply equations of the form y² = x³ + ax + b. Some graphs of what these can look like are shown below. This discovery was the mathematical equivalent of realising that the instructions for building life were encoded in strands of DNA.  

Although the Taniyama-Shimura conjecture was a beautiful hypothesis, nobody could prove it was true for every elliptic equation and every modular form. Crucially, if the Taniyama-Shimura conjecture could be proven, it could be used to prove dozens of other conjectures. It became one of the holy grails of 20th-century number theory.

Then was another 30 years with no progress on Fermat’s last theorem until 1986, Ken Ribet, a professor at the University of California, Berkeley, was attending the International Congress of Mathematicians when he had a revelation. He proved that a consequence of the Taniyama- Shimura conjecture being true was that Fermat’s Last Theorem was also true. Therefore, mathematicians had a concrete way to prove Fermat’s last theorem, prove the Taniyama-Shimura conjecture. The only problem was it was believed that the Taniyama-Shimura conjecture was impossible to prove.

However, there was one person who, when hearing of Ribet’s discovery believed he could solve this conjecture and that was Andrew Wiles. At the time he was a Professor at Princeton University. He had been fascinated with Fermat’s last theorem since age 10 and it had been his life’s ambition to solve the problem. He set out to solve the problem, but did so in secret. He put himself into isolation for 7 years trying to find a solution, telling no one what he was doing.

In 1993 Wiles announced a lecture series with the devious title ‘Modular Elliptic Curves.’ It was leaked to the mathematical community that something special was to happen at this event. Throughout the lecture Wiles showed how he had discovered a way to count modular forms, by grouping them in a certain way. He used this to check each group was related to an elliptic curve. This proved the Taniyama-Shimura conjecture which proved Fermat’s last theorem.

An interesting point is, was Wiles’ proof the same as Fermat’s? This is definitely no. Wiles’ proof was a twentieth century proof and relied on many ideas Fermat would not have known. We actually believe that Fermat although correct, was mistaken that he had a proof for his theorem. Fermat’s last theorem still excites people today, including me, which is why I have slipped in the equation below. Interesting?

386692⁷ + 411413⁷ = 441849⁷

To find out more about Fermat’s last theorem I would highly recommended the BBC horizon documentary. It is presented by top Mathematicians from across the globe and they present it with all the relevant maths and explain everything superbly. Also none of the maths is too technical for even a GCSE student to understand so I would really recommend this programme. This makes this programme much better than the popular fiction on Fermat’s last theorem, because a lot of popular fiction is too hard when it doesn’t need to be and sometimes inaccurate. My personal favourite part was hearing from Goro Shimura whose reaction to finding out his theorem was true was apparently to send a fax to every mathematician at most universities across the globe saying 'I told you so'

I hope you enjoyed that short introduction into Fermat's Last Theorem. I will soon upload the proof for my most recent puzzle, so keep trying to solve it if you haven't finished. Finally, thank you again for Reading.